The internet has been talking about a list of AI papers that Ilya Sutskever, co-founder of OpenAI, recommended to John Carmack:

“So I asked Ilya, their chief scientist, for a reading list. This is my path, my way of doing things: give me a stack of all the stuff I need to know to actually be relevant in this space. And he gave me a list of like 40 research papers and said, ‘If you really learn all of these, you’ll know 90% of what matters today.’ And I did. I plowed through all those things and it all started sorting out in my head.”

The exact list seems to be lost to time, but something like it recently resurfaced on Xwitter. Regardless of origin, the list includes some interesting papers in the development of large language models — i.e., the class of artificial neural networks responsible for things like ChatGPT. Together, they tell a story of how we learned to assemble basic neural units into increasingly sophisticated architectures, what those architectures are capable of learning, and the practical techniques that make training them possible.

“Ilya’s List” of AI Papers

I’ve collected the papers here, along with some key takeaways from each. They are in chronological order to make it easier to see how they build on each other. Most are papers, but a few are books, blog posts, course notes, etc. In any case, it’s a lot of reading! I’ve highlighted a few that I think are particularly worth a look.

Keeping Neural Networks Simple by Minimizing the Description Length of the Weights

Hinton, Geoffrey E., and Drew Van Camp, 1993 (PDF)

“Supervised neural networks generalize well if there is much less information in the weights than there is in the output vectors of the training cases. So during learning, it is important to keep the weights simple by penalizing the amount of information they contain. The amount of information in a weight can be controlled by adding Gaussian noise and the noise level can be adapted during learning to optimize the trade-off between the expected squared error of the network and the amount of information in the weights. We describe a method of computing the derivatives of the expected squared error and of the amount of information in the noisy weights in a network that contains a layer of non-linear hidden units. Provided the output units are linear, the exact derivatives can be computed efficiently without time-consuming Monte Carlo simulations. The idea of minimizing the amount of information that is required to communicate the weights of a neural network leads to a number of interesting schemes for encoding the weights”

Takeaways

The Minimum Description Length Principle asserts that the best model of some data is the one that minimizes the sum of the length of the description of the model and the length of the data encoded using that model.

  • Applies the MDL principle to neural networks to control model complexity and prevent overfitting.
  • Uses weight-sharing to minimize the description length of the weights: The same weight is applied to multiple connections in the network, reducing the number of free parameters, and thus the model complexity.

A Tutorial Introduction to the Minimum Description Length Principle

Peter Grünwald, 2004 (PDF)

Takeaways

A clearly-written intro to the Minimum Description Length Principle and its applications to model selection.

  • Learning as data compression Every regularity in data may be used to compress that data, and learning can be equated with finding those regularities.
  • MDL as model selection The best model is the one that minimizes the sum of the length of the description of the model and the length of the data encoded using that model.

Machine Super Intelligence

Legg, Shane, 2008 (PDF)

This thesis sets out to define what it means for an agent to be intelligent. Starting from informal definitions of intelligence, it mathematically defines intelligence in a general, powerful, and elegant way. This leads to the concept of an optimal agent that maximizes its expected reward by interacting with an unknown environment. While not a practical theory – it’s definitions are not computable – it maybe provides a theoretical framework for understanding real, suboptimal agents.

Takeaways

  • “Intelligence measures an agent’s ability to achieve goals in a wide range of environments.”
  • The complexity of an environment is the length of the shortest program that generates the environment’s behavior (Kolmogorov complexity).
  • Prior probability of an environment decreases exponentially with its complexity (Algorithmic probability). This formalizes Occam’s razor.
  • The Universal Intelligence of an agent is the expected value of its rewards.
  • Perfect or “universal agents” maximize their expected reward in any computable environment. While not computable (because Kolmogorov complexity is uncomputable), it provides a theoretical upper bound on the intelligence of computable agents.

The First Law of Complexodynamics

Scott Aaronson, 2011. (Blog Post)

Takeaways

Theoretical computer scientist Scott Aaronson (complexity theory, quantum computing) tries to pin down what we mean by “complex systems”, and conjectures about what it would mean to define complexity in a rigorous way. He pulls in concepts like entropy and (resource-bounded) Kolmogorov complexity. There are some interesting questions here, but feel free to skip this one if you are looking for practical takeaways.

ImageNet Classification with Deep Convolutional Neural Networks

Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton, 2012 (PDF)

“We trained a large, deep convolutional neural network to classify the 1.2 million high-resolution images in the ImageNet LSVRC-2010 contest into the 1000 different classes. On the test data, we achieved top-1 and top-5 error rates of 37.5% and 17.0% which is considerably better than the previous state-of-the-art. The neural network, which has 60 million parameters and 650,000 neurons, consists of five convolutional layers, some of which are followed by max-pooling layers, and three fully-connected layers with a final 1000-way softmax. To make training faster, we used non-saturating neurons and a very efficient GPU implementation of the convolution operation. To reduce overfitting in the fully-connected layers we employed a recently-developed regularization method called “dropout” that proved to be very effective. We also entered a variant of this model in the ILSVRC-2012 competition and achieved a winning top-5 test error rate of 15.3%, compared to 26.2% achieved by the second-best entry.”

Takeaways

  • Introduced AlexNet, a deep convolutional neural network that achieved unprecedented performance in image classification. AlexNet won the ImageNet Large Scale Visual Recognition Challenge in 2012 by a substantial margin, bringing deep learning to the forefront of computer vision research.
  • Deep Architecture AlexNet’s depth – five convolutional and three fully connected layers – allowed the network to learn hierarchical feature representations, capturing complex patterns in the data that were not possible with shallower architectures.
  • Training with GPUs Used GPUs, parallel computation, and ReLU activation functions to speed up training.

Neural Turing Machines

Graves, Alex, Greg Wayne, and Ivo Danihelka, 2014 (PDF)

“We extend the capabilities of neural networks by coupling them to external memory resources, which they can interact with by attentional processes. The combined system is analogous to a Turing Machine or Von Neumann architecture but is differentiable end-to-end, allowing it to be efficiently trained with gradient descent. Preliminary results demonstrate that Neural Turing Machines can infer simple algorithms such as copying, sorting, and associative recall from input and output examples”

Takeaways

  • Neural Turing Machines are fully differentiable computers that learn their own programming. Differentiability is the key to efficiently training NTMs with gradient descent.
  • Augmenting a NN with external memory addresses a key limitation of vanilla RNNs: their inability to store information for long periods of time.
  • Earlier work showed that RNNs are Turing Complete, meaning that in principle they are capable of learning algorithms from examples, but didn’t show how to actually do it.

Quantifying the Rise and Fall of Complexity in Closed Systems

Aaronson, Carroll, Ouelette, 2014 (PDF)

“In contrast to entropy, which increases monotonically, the “complexity” or “interestingness” of closed systems seems intuitively to increase at first and then decrease as equilibrium is approached. For example, our universe lacked complex structures at the Big Bang and will also lack them after black holes evaporate and particles are dispersed. This paper makes an initial attempt to quantify this pattern. As a model system, we use a simple, two-dimensional cellular automaton that simulates the mixing of two liquids (“coffee” and “cream”). A plausible complexity measure is then the Kolmogorov complexity of a coarse-grained approximation of the automaton’s state, which we dub the “apparent complexity.” We study this complexity measure, and show analytically that it never becomes large when the liquid particles are noninteracting. By contrast, when the particles do interact, we give numerical evidence that the complexity reaches a maximum comparable to the “coffee cup’s” horizontal dimension. We raise the problem of proving this behavior analytically.”

Takeaways

This paper continues ideas from The First Law of Complexodynamics. I think you can safely skip it.

  • The entropy of an n-bit string is often identified with its Kolmogorov complexity, i.e., the length of the shortest program that generates the string.
  • Kolmogorov complexity is well-known to be uncomputable (equivalent to the halting problem), but can maybe be approximated? “While Kolmogorov complexity and sophistication are useful theoretical notions to model our ideas of entropy and complexity, they cannot be directly applied in numerical simulations, because they are both uncomputable.”

Deep Residual Learning for Image Recognition

He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun, 2015 (PDF)

“Deeper neural networks are more difficult to train. We present a residual learning framework to ease the training of networks that are substantially deeper than those used previously. We explicitly reformulate the layers as learning residual functions with reference to the layer inputs, instead of learning unreferenced functions. We provide comprehensive empirical evidence showing that these residual networks are easier to optimize, and can gain accuracy from considerably increased depth. On the ImageNet dataset we evaluate residual nets with a depth of up to 152 layers—8x deeper than VGG nets but still having lower complexity. An ensemble of these residual nets achieves 3.57% error on the ImageNet test set. This result won the 1st place on the ILSVRC 2015 classification task. We also present analysis on CIFAR-10 with 100 and 1000 layers. The depth of representations is of central importance for many visual recognition tasks. Solely due to our extremely deep representations, we obtain a 28% relative improvement on the COCO object detection dataset. Deep residual nets are foundations of our submissions to ILSVRC & COCO 2015 competitions, where we also won the 1st places on the tasks of ImageNet detection, ImageNet localization, COCO detection, and COCO segmentation.”

Takeaways

  • Degradation Problem: Additional layers can increase both testing and training error, i.e., not just overfitting. This is counterintuitive because deeper networks could just represent shallower networks by setting some layers to the identity function.
  • Introduces Residual Networks (ResNets). The core idea is skip connections that bypass one or more layers so that layers represent the residual function F(x) = H(x) - x.

Neural Machine Translation by Jointly Learning to Align and Translate

Bahdanau, Dzmitry, Kyunghyun Cho, and Yoshua Bengio, 2015 (PDF)

“Neural machine translation is a recently proposed approach to machine translation. Unlike the traditional statistical machine translation, the neural machine translation aims at building a single neural network that can be jointly tuned to maximize the translation performance. The models proposed recently for neural machine translation often belong to a family of encoder-decoders and consists of an encoder that encodes a source sentence into a fixed-length vector from which a decoder generates a translation. In this paper, we conjecture that the use of a fixed-length vector is a bottleneck in improving the performance of this basic encoder-decoder architecture, and propose to extend this by allowing a model to automatically (soft-)search for parts of a source sentence that are relevant to predicting a target word, without having to form these parts as a hard segment explicitly. With this new approach, we achieve a translation performance comparable to the existing state-of-the-art phrase-based system on the task of English-to-French translation. Furthermore, qualitative analysis reveals that the (soft-)alignments found by the model agree well with our intuition.”

Takeaways

  • Introduces the Attention Mechanism, a major breakthrough in machine translation and many other sequence-to-sequence tasks. The attention mechanism allows the model to focus on different parts of the source sentence while generating each word in the target sentence, addressing the limitations of fixed-length context vectors in previous encoder-decoder architectures.

Pointer Networks

Oriol Vinyals, Meire Fortunato, Navdeep Jaitly. 2015 (PDF)

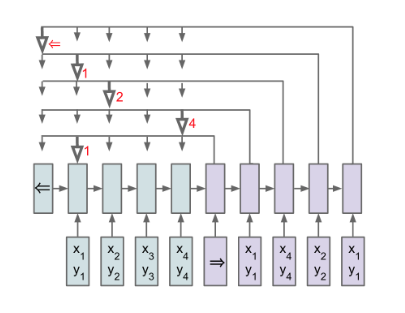
Pointer Network

“We introduce a new neural architecture to learn the conditional probability of an output sequence with elements that are discrete tokens corresponding to positions in an input sequence. Such problems cannot be trivially addressed by existent approaches such as sequence-to-sequence and Neural Turing Machines, because the number of target classes in each step of the output depends on the length of the input, which is variable. Problems such as sorting variable sized sequences, and various combinatorial optimization problems belong to this class. Our model solves the problem of variable size output dictionaries using a recently proposed mechanism of neural attention. It differs from the previous attention attempts in that, instead of using attention to blend hidden units of an encoder to a context vector at each decoder step, it uses attention as a pointer to select a member of the input sequence as the output. We call this architecture a Pointer Net (Ptr-Net). We show Ptr-Nets can be used to learn approximate solutions to three challenging geometric problems – finding planar convex hulls, computing Delaunay triangulations, and the planar Travelling Salesman Problem – using training examples alone. Ptr-Nets not only improve over sequence-to-sequence with input attention, but also allow us to generalize to variable size output dictionaries. We show that the learnt models generalize beyond the maximum lengths they were trained on. We hope our results on these tasks will encourage a broader exploration of neural learning for discrete problems.”

Takeaways

  • Variable Output Dictionaries: The number of target classes in each step of the output depends on the length of the input, which is variable. Conventional sequence-to-sequence models require a fixed output vocabulary.
  • At each step of the output, the model uses attention over the inputs as a pointer to select a member of the input sequence as the output. This allows the model to generalize to variable size output dictionaries.

Recurrent Neural Network Regularization

Zaremba, Sutskever, Vinyals. 2015 (PDF)

“We present a simple regularization technique for Recurrent Neural Networks (RNNs) with Long Short-Term Memory (LSTM) units. Dropout, the most successful technique for regularizing neural networks, does not work well with RNNs and LSTMs. In this paper, we show how to correctly apply dropout to LSTMs, and show that it substantially reduces overfitting on a variety of tasks. These tasks include language modeling, speech recognition, image caption generation, and machine translation.”

Takeaways

  • Applies dropout only to a subset of the RNNs connections.
  • “By not using dropout on the recurrent connections, the LSTM can benefit from dropout regularization without sacrificing its valuable memorization ability.”

The Unreasonable Effectiveness of Recurrent Neural Networks

Andrej Karpathy, 2015 (Blog Post)

This blog post from one of the OpenAI co-founders is a great introduction to the power of Recurrent Neural Networks (RNNs) for sequence modeling. It shows that RNNs are deceptively simple, and demonstrates the power of RNNs to generate reasonable text using only character-by-character predictions. It’s fun to see where generative language models were just a few years ago, and how far they’ve come since.

Takeaways

  • “If training vanilla neural nets is optimization over functions, training recurrent nets is optimization over programs.”
  • Feed-Forward Neural Networks are limited to fixed-sized inputs and fixed-size outputs.
  • RNNs operate on sequences of arbitrary length, making them well-suited for speech recognition, language modeling, and machine translation.

Understanding LSTM Networks

Christopher Olah, 2015 (Blog Post)

This blog post from one of the co-founders of Anthropic is a great introduction to an important type of RNN called Long Short-Term Memory (LSTM) networks. In a step-by-step fashion, it explains how the different “gates” of an LSTM unit work together to store and retrieve information.

Takeaways

  • LSTMs improve on RNNs by adding a piece of hidden state called a memory cell that can store information for long periods of time. This improves their ability to learn from long sequences, and makes them well-suited to natural language processing. In contrast, regular RNNs struggle to connect separate pieces of information, say, words that are far apart in a sentence.
  • An LSTM unit contains a memory cell, an input gate, an output gate and a forget gate that regulate the flow of information in and out of the memory cell.
  • Interesting to see an idea (LSTMs) from 1997 returning to the forefront of research activity in 2015. Plenty of things happened in those 18 years, including some pretty dramatic increases in computational power.

Deep Speech 2: End-to-End Speech Recognition in English and Mandarin

Amodei, et al. 2016 (PDF)

“We show that an end-to-end deep learning approach can be used to recognize either English or Mandarin Chinese speech-two vastly different languages. Because it replaces entire pipelines of hand-engineered components with neural networks, end-to-end learning allows us to handle a diverse variety of speech including noisy environments, accents and different languages. Key to our approach is our application of HPC techniques, enabling experiments that previously took weeks to now run in days. This allows us to iterate more quickly to identify superior architectures and algorithms. As a result, in several cases, our system is competitive with the transcription of human workers when benchmarked on standard datasets. Finally, using a technique called Batch Dispatch with GPUs in the data center, we show that our system can be inexpensively deployed in an online setting, delivering low latency when serving users at scale.”

Takeaways

  • End-to-End Learning replaces entire pipelines of hand-engineered components (features, acoustic models, language models, etc.) with neural networks. This is demonstrated on two very different languages: English and Mandarin.
  • Highly-optimized training system with 8 or 16 GPUs.
  • Models have around 100 million parameters.

Identity Mappings in Deep Residual Networks

Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun. 2016 (PDF)

“Deep residual networks have emerged as a family of extremely deep architectures showing compelling accuracy and nice convergence behaviors. In this paper, we analyze the propagation formulations behind the residual building blocks, which suggest that the forward and backward signals can be directly propagated from one block to any other block, when using identity mappings as the skip connections and after-addition activation. A series of ablation experiments support the importance of these identity mappings. This motivates us to propose a new residual unit, which makes training easier and improves generalization. We report improved results using a 1001-layer ResNet on CIFAR-10 (4.62% error) and CIFAR-100, and a 200-layer ResNet on ImageNet.”

Takeaways

  • The authors build on their previous paper, Deep Residual Learning for Image Recognition, and propose a new residual unit by setting some parts of the original residual unit to identity mappings. The result is a “residual relation” between every pair of layers, which gives the forward and backward signals a nice, additive structure.
  • Demonstrates new residual units in a 1001-layer ResNet.

Multi-Scale Context Aggregation by Dilated Convolutions

Fisher Yu, Vladlen Koltun. 2015 (PDF)

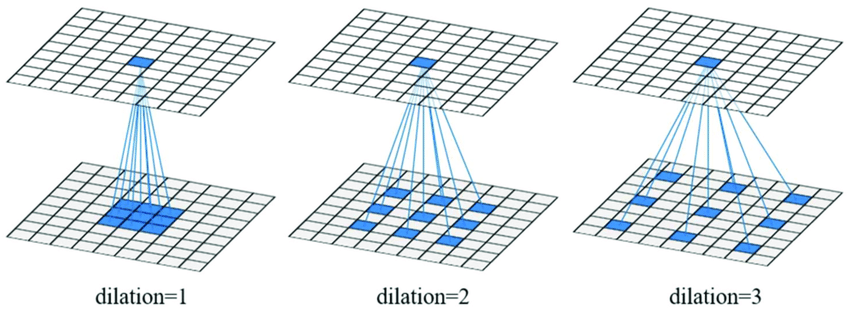
State-of-the-art models for semantic segmentation are based on adaptations of convolutional networks that had originally been designed for image classification. However, dense prediction and image classification are structurally different. In this work, we develop a new convolutional network module that is specifically designed for dense prediction. The presented module uses dilated convolutions to systematically aggregate multi-scale contextual information without losing resolution. The architecture is based on the fact that dilated convolutions support exponential expansion of the receptive field without loss of resolution or coverage. We show that the presented context module increases the accuracy of state-of-the-art semantic segmentation systems. In addition, we examine the adaptation of image classification networks to dense prediction and show that simplifying the adapted network can increase accuracy.

Takeaways

  • Semantic segmentation assigns a label to each pixel in the image. This is a different task from image classification, where the goal is to assign a single label to the entire image. However, many semantic segmentation models are based on architectures designed for image classification.
  • Critically evaluates techniques borrowed from image classification and finds that pooling and subsampling layers may not be a good fit for semantic segmentation.
  • Advocates for dilated convolutions - a type of convolution with gaps between the kernel elements. This expands the receptive field without increasing the number of parameters.

Zeebra

Order Matters: Sequence to sequence for sets

Oriol Vinyals, Samy Bengio, Manjunath Kudlur. 2015 (PDF)

“Sequences have become first class citizens in supervised learning thanks to the resurgence of recurrent neural networks. Many complex tasks that require mapping from or to a sequence of observations can now be formulated with the sequence-to-sequence (seq2seq) framework which employs the chain rule to efficiently represent the joint probability of sequences. In many cases, however, variable sized inputs and/or outputs might not be naturally expressed as sequences. For instance, it is not clear how to input a set of numbers into a model where the task is to sort them; similarly, we do not know how to organize outputs when they correspond to random variables and the task is to model their unknown joint probability. In this paper, we first show using various examples that the order in which we organize input and/or output data matters significantly when learning an underlying model. We then discuss an extension of the seq2seq framework that goes beyond sequences and handles input sets in a principled way. In addition, we propose a loss which, by searching over possible orders during training, deals with the lack of structure of output sets. We show empirical evidence of our claims regarding ordering, and on the modifications to the seq2seq framework on benchmark language modeling and parsing tasks, as well as two artificial tasks – sorting numbers and estimating the joint probability of unknown graphical models.”

Takeaways

  • Seq2Seq models are inherently order-sensitive, but tasks like sorting are inherently not order-sensitive.
  • Read-Process-Write creates a permutation-invariant embedding of the input. This is fed to an LSTM Pointer Network
  • Handles unordered output by searching over possible orders during training. This feels funky…

Variational Lossy Autoencoder

Chen, et al. 2016 (PDF)

“Representation learning seeks to expose certain aspects of observed data in a learned representation that’s amenable to downstream tasks like classification. For instance, a good representation for 2D images might be one that describes only global structure and discards information about detailed texture. In this paper, we present a simple but principled method to learn such global representations by combining Variational Autoencoder (VAE) with neural autoregressive models such as RNN, MADE and PixelRNN/CNN. Our proposed VAE model allows us to have control over what the global latent code can learn and, by designing the architecture accordingly, we can force the global latent code to discard irrelevant information such as texture in 2D images, and hence the VAE only “autoencodes” data in a lossy fashion. In addition, by leveraging autoregressive models as both prior distribution p(z) and decoding distribution p(x|z), we can greatly improve generative modeling performance of VAEs, achieving new state-of-the-art results on MNIST, OMNIGLOT and Caltech-101 Silhouettes density estimation tasks.”

Takeaways

  • TODO

A Simple Neural Network Module for Relational Reasoning

Santoro, et al. 2017 (PDF)

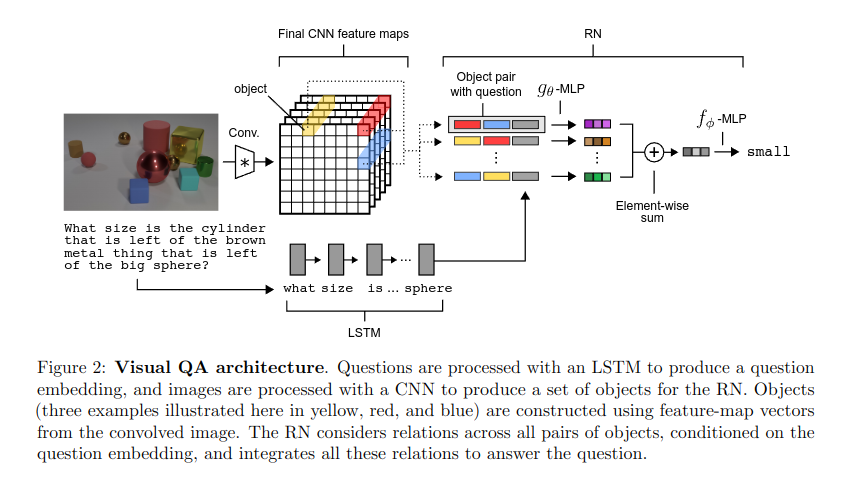
Relational Reasoning

“Relational reasoning is a central component of generally intelligent behavior, but has proven difficult for neural networks to learn. In this paper we describe how to use Relation Networks (RNs) as a simple plug-and-play module to solve problems that fundamentally hinge on relational reasoning. We tested RN-augmented networks on three tasks: visual question answering using a challenging dataset called CLEVR, on which we achieve state-of-the-art, super-human performance; text-based question answering using the bAbI suite of tasks; and complex reasoning about dynamic physical systems. Then, using a curated dataset called Sort-of-CLEVR we show that powerful convolutional networks do not have a general capacity to solve relational questions, but can gain this capacity when augmented with RNs. Our work shows how a deep learning architecture equipped with an RN module can implicitly discover and learn to reason about entities and their relations.”

Takeaways

  • Relational reasoning is the ability to understand, infer, and manipulate the relationships between different entities or pieces of information.
  • Achieves super-human performance on the CLEVR visual reasoning task.
  • RNs constrain the functional form of a NN so that it captures common properties of relational reasoning, in the same way that convolutional layers capture translational invariance, or recurrent layers capture sequential dependencies.
  • RNs operate on a set of objects, and learn (pairwise) relations between them.

Attention is All You Need

Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, Polosukhin. 2017

(Helpfully Annotated Paper) (Original Paper)

“The dominant sequence transduction models are based on complex recurrent or convolutional neural networks that include an encoder and a decoder. The best performing models also connect the encoder and decoder through an attention mechanism. We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely. Experiments on two machine translation tasks show…”

Takeaways

  • Transformer architecture removes the recurrent (sequential) connections of RNNs. This allows efficient, parallel training with GPUs.
  • The self-attention mechanism enables the model to weigh the importance of different words in a sentence, regardless of their position. This allows for capturing long-range dependencies and relationships more effectively than RNNs.

Kolmogorov Complexity and Algorithmic Randomness

“Looking at a sequence of zeros and ones, we often feel that it is not random, that is, it is not plausible as an outcome of fair coin tossing. Why? The answer is provided by algorithmic information theory: because the sequence is compressible, that is, it has small complexity or, equivalently, can be produced by a short program. This idea, going back to Solomonoff, Kolmogorov, Chaitin, Levin, and others, is now the starting point of algorithmic information theory. The first part of this book is a textbook-style exposition of the basic notions of complexity and randomness; the second part covers some recent work done by participants of the “Kolmogorov seminar” in Moscow (started by Kolmogorov himself in the 1980s) and their colleagues.”

(PDF)

This is a substantial book, and I’ve only skimmed it. I’d suggest looking at An Introduction to Kolmogorov Complexity and Its Applications instead.

Takeaways

  • Kolmogorov Complexity is a universal definition for the complexity, or quantity of information, in an object.
  • This differs from Shannon’s Entropy, which is the amount of information that needs to be communicated in order to select an object from a known list of alternatives (symbols).

Neural Message Passing for Quantum Chemistry

Gilmer, et al. 2017(PDF)

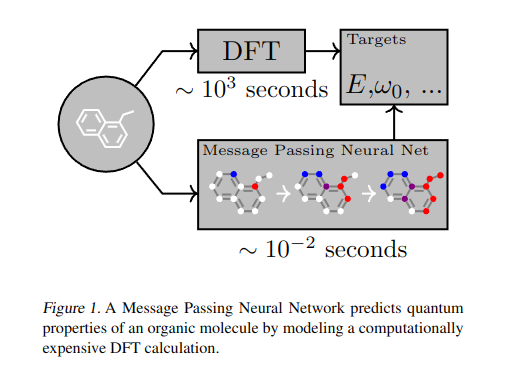
Message Passing Neural Networks

“Supervised learning on molecules has incredible potential to be useful in chemistry, drug discovery, and materials science. Luckily, several promising and closely related neural network models invariant to molecular symmetries have already been described in the literature. These models learn a message passing algorithm and aggregation procedure to compute a function of their entire input graph. At this point, the next step is to find a particularly effective variant of this general approach and apply it to chemical prediction benchmarks until we either solve them or reach the limits of the approach. In this paper, we reformulate existing models into a single common framework we call Message Passing Neural Networks (MPNNs) and explore additional novel variations within this framework. Using MPNNs we demonstrate state of the art results on an important molecular property prediction benchmark; these results are strong enough that we believe future work should focus on datasets with larger molecules or more accurate ground truth labels.”

Takeaways

  • Message Passing Neural Networks (MPNNs) abstracts commonalities of several models for graph-based data. Nodes iteratively pass messages to their neighbors, who aggregate these messages and update their own state. Finally, a readout function maps the final node states to the graph’s global state.
  • Uses set2set to produce a readout that is invariant to graph order.

Relational Recurrent Neural Networks

Santoro, Adam, et al. 2018 (PDF)

“Memory-based neural networks model temporal data by leveraging an ability to remember information for long periods. It is unclear, however, whether they also have an ability to perform complex relational reasoning with the information they remember. Here, we first confirm our intuitions that standard memory architectures may struggle at tasks that heavily involve an understanding of the ways in which entities are connected – i.e., tasks involving relational reasoning. We then improve upon these deficits by using a new memory module – a Relational Memory Core (RMC) – which employs multi-head dot product attention to allow memories to interact. Finally, we test the RMC on a suite of tasks that may profit from more capable relational reasoning across sequential information, and show large gains in RL domains (e.g. Mini PacMan), program evaluation, and language modeling, achieving state-of-the-art results on the WikiText-103, Project Gutenberg, and GigaWord datasets.”

Takeaways

  • “[A]n architectural backbone upon which a model can learn to compartmentalize information, and learn to compute interactions between compartmentalized information.”
  • Relational Memory Core (RMC) maintains a matrix of row-wise memories. Updates are via attention over previous memories and input.
  • The memory matrix can be viewed as the matrix of cell states in a 2D-LSTM.

GPipe: Efficient Training of Giant Neural Networks using Pipeline Parallelism

Hung, et al. 2018 (PDF) (Blog)

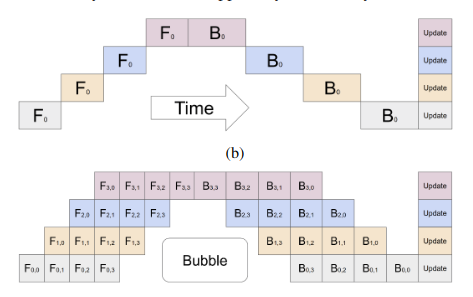
Micro-batch pipelining

“Scaling up deep neural network capacity has been known as an effective approach to improving model quality for several different machine learning tasks. In many cases, increasing model capacity beyond the memory limit of a single accelerator has required developing special algorithms or infrastructure. These solutions are often architecture-specific and do not transfer to other tasks. To address the need for efficient and task-independent model parallelism, we introduce GPipe, a pipeline parallelism library that allows scaling any network that can be expressed as a sequence of layers. By pipelining different sub-sequences of layers on separate accelerators, GPipe provides the flexibility of scaling a variety of different networks to gigantic sizes efficiently. Moreover, GPipe utilizes a novel batch-splitting pipelining algorithm, resulting in almost linear speedup when a model is partitioned across multiple accelerators. We demonstrate the advantages of GPipe by training large-scale neural networks on two different tasks with distinct network architectures: (i) Image Classification: We train a 557-million-parameter AmoebaNet model and attain a top-1 accuracy of 84.4% on ImageNet-2012, (ii) Multilingual Neural Machine Translation: We train a single 6-billion-parameter, 128-layer Transformer model on a corpus spanning over 100 languages and achieve better quality than all bilingual models.”

Takeaways

  • Increasing model size generally improves model performance, but model growth is outstripping hardware growth.
  • GPipe is a distributed machine learning library that uses synchronous stochastic gradient descent and pipeline parallelism for training on multiple accelerators.
  • Forward pass: mini-batches are split into micro-batches and pipelined across accelerators. Backward pass: gradients are accumulated across micro-batches.

Scaling Laws for Neural Language Models

Kaplan, et al. 2020 (PDF)

“We study empirical scaling laws for language model performance on the cross-entropy loss. The loss scales as a power-law with model size, dataset size, and the amount of compute used for training, with some trends spanning more than seven orders of magnitude. Other architectural details such as network width or depth have minimal effects within a wide range. Simple equations govern the dependence of overfitting on model/dataset size and the dependence of training speed on model size. These relationships allow us to determine the optimal allocation of a fixed compute budget. Larger models are significantly more sample-efficient, such that optimally compute-efficient training involves training very large models on a relatively modest amount of data and stopping significantly before convergence.”

Takeaways

  • “Language modeling performance improves smoothly and predictably as we appropriately scale up model size, data, and compute.”
  • Language model (Transformer) performance depends most strongly on scale: model size, dataset size, and compute resources.
  • Performance has a smooth power-law relationship with each scale factor (implying diminishing marginal returns with increasing scale).
  • Performance has “very weak dependence on many architectural and optimization hyper-parameters.”
  • “Our results strongly suggest that larger models will continue to perform better, and will also be much more sample efficient than has been previously appreciated. Big models may be more important than big data.”

CAVEAT: Not everyone agrees with these scaling laws.

CS231n Convolutional Neural Networks for Visual Recognition

(2024 Course Notes)

“This course is a deep dive into the details of deep learning architectures with a focus on learning end-to-end models for these tasks, particularly image classification.”

Takeaways

The course notes contain excellent treatment of the fundamentals of neural networks, including:

<
Previous Post
Zeebra: ZEro-knowledge algEBRA
>
Next Post
Deep Learning: Autoencoders